Bijaganitavatamsa ("The Crown of Algebra")
Book Specification
| Item Code: | UAB883 |
| Author: | Venugopal D. Heroor |
| Publisher: | Kavi Kulaguru Kalidas Sanskrit University |
| Language: | English |
| Edition: | 2019 |
| ISBN: | 9789385710193 |
| Pages: | 269 |
| Cover: | PAPERBACK |
| Other Details | 8.50X5.50 inch Depth |
| Weight | 350 gm |
Book Description
The present work contains the Sanskrit text of Bījaganitāvatamsa of Nārāyaṇa Pandita with Introduction, English translation, exposition, notes, rationales of the rules, and complete solution of illustrative examples according to the methods of Närāyaṇa using modern symbols.
Bijaganitāvatamsa ["The Crown of Algebra"] is a mathematical work, written in Sanskrit, by Närāyaṇa Pandita(1356 A.D.). A crtical edition of the work, availabale now, in printed form, edited by Kripa Shankar Shukla and published by Akhila Bharatiya Sanskrit Parishad, Lucknow, in 1970, is based on an incomplete manuscript containing the whole of Part I and a few opening lines of part II.
Like other Hindu works on algebra, it is divided into two parts, Part I dealing with algebraic-processes essential in solving algebraic equations (bijjopayogi-ganita) and Part II dealing with algebraic equations (bija).
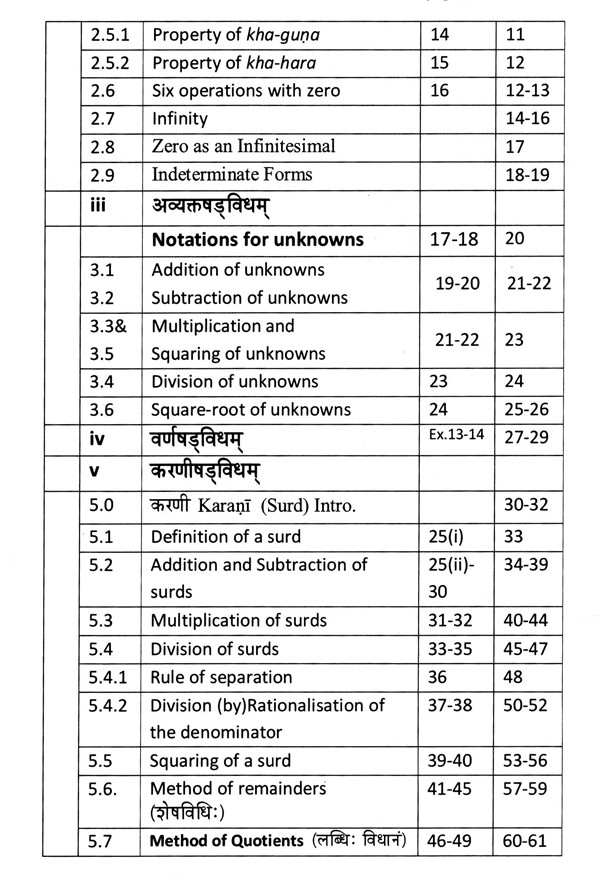
Part I sets forth the following three topics:
(1) Algebraic operations (of addition, subtraction, multiplication, division, squaring and extracting the square-root) for each of the following:
(i) Positive and negative numbers (dhanarna),
(ii) The zero (sūnya),
(iii) Single unknown (avyakta),
(iv) More unknowns characterized by colours (varna),
(v). surds (karani).
The method for finding the square root of a surd of the type (a + √b + √c + √d ) as given in Rule 46-49, and the method of finding the approximate values of the square-root of a non square number (quadratic surd) as given in rule 86, were given by Närāyaṇa Pandita for the first time; and are note worthy.
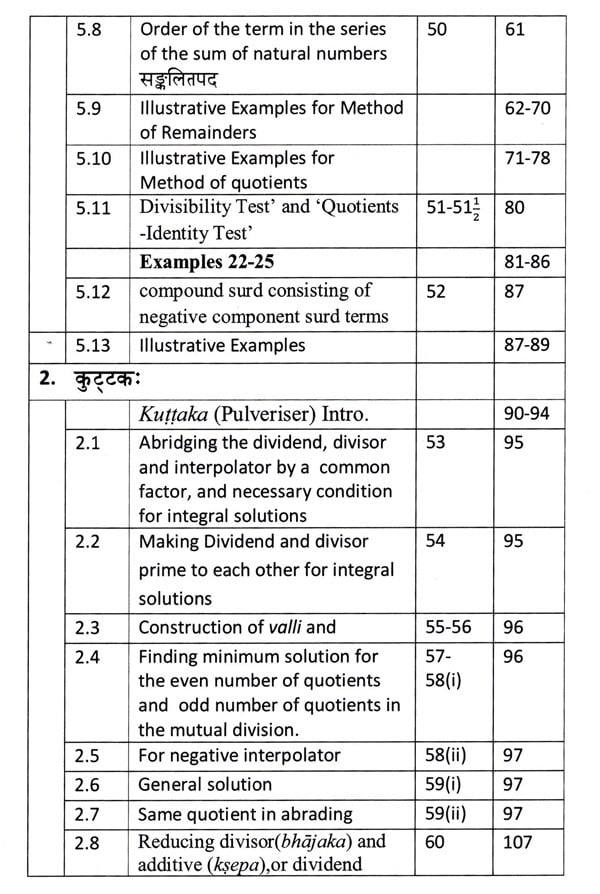
(2) The Pulveriser (kuttaka), i.e. analysis pertaining to the indeterminate equation : (ax + c)/b = y.
Though the chapter on pulveriser in both the books Ganitakaumudi and Bijaganitāvatamsa, by the same author, is nearly the same, two rules [for the solution of the pulveriser when the solution is fractional viz. rule 68 and 69 ], an example [Ex. 36] and a comment available in this book is not available in the former one. A set of four Sūtras [R.32-36(i)], followed by six examples (Ex.30-35) dealing with the residual and conjunct pulverisers sāgrakuttaka and samślişta- kuttaka occuring (between verses 64 and 65) in Ganitakaumudi are not found here in Bījaganitāvatāmsa. So they have been included here in Appendix-1.
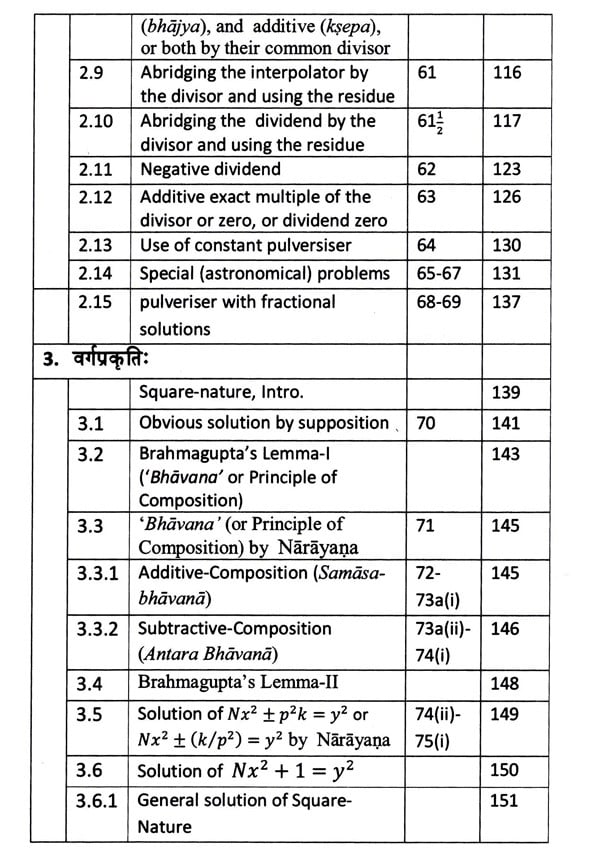
(3) The Square-nature (varga-prakrti), i. e., analysis pertaining to the indeterminate equation : Nx² + c = y².
It is mentioned by the editor, that the manuscript breaks off after giving the list of contents of Part II and an example of a linear equation in one unknown.
The Sanskrit text as found in the printed form, edited by Kripa Shankar Shukla (mentioned above) is adopted here. In the translation, the portion of English translation of verses available in the History Of Hindu Mathematics part -II (Algebra) by Bibhutibhusan Datta and Avadhes Narayan Singh is reproduced as it is. Occasionally, English translation of Ganitakaumudi by Paramananad Singh have also been reffered. Regarding the explanation part and rationale of rules some intermediary steps are added wherever found necessary. Complete solution of illustrative examples according to the methods of Näräyaṇa Pandita using modern symbols is given and the answers obtained are verified to facilitate the readers in general, students and Sanskrit scholars with elementary knowledge of mathematics in particular.
Parallel rules and similar examples found in other available works on Hindu mathematics have been indicated in the translation and foot notes. Heading and sub-headings have been provided to facilitate consultation.
I have been indebted to and relied on the expository source works by great savants like Bibhutibhushan Datta, A.N. Singh, K.S. Shukla, and Paramananad Singh. Works of Datta and Singh have been the main source of inspiration for me in this work. I express my sincere gratitude to all those stawarts in the field.
I am grateful to Prof. Shrinivasa Varkhedi, VC, for gracing this book with his valuable foreword and also thanks to Prof. Madhusudan Penna, Director, Publication, Kavikulaguru Kalidas Sanskrit University for including this book in University Publications.
I express my thanks and appreciation to Dr. Renuka Bokare, PRO for publication support and Shri. Umesh Patil, Sr. Clerk, KKSU for the cover page design.
I express my profound gratitude to authorities of Kavikulaguru Kalidas Sanskrit University for taking up the task of publishing the work.
The author hopes that this book will be quite useful and interesting to the students and researchers in the field of Indian Mathematics.
The present work, Bijaganitāvatamsa, of Nārāyaṇa Pandita contains the Sanskrit text with Introduction, English translation, exposition, notes, rationales of the rules, and complete solution of illustrative examples according to the methods of Nārāyaṇa using modern symbols.
Nārāyaṇa Daivajña or Nārāyaṇa Pandita as he was popularly called, was the son of Nrsimha Daivajña. He is solely a mathematician and the author of two works namely (i) Ganitakaumudi (G.K.) a mathematical treatise in 14 chapters, and (ii) Bījaganitāvatamsa a work on algebra. Besides these two works, Nārāyaṇa has also written a work on Sanskrit prosody viz. Manimanjarī on Sanskrit prosody. Närāyaṇa Pandita lived in the fourteenth century of the Christian era.
Bijaganitāvatamsa is a mathematical work, written in Sanskrit, by Närāyaṇa Pandita (1356 C.E.). The name Bijaganitāvatamsa is a compound formed by the composition of the words bijaganita, meaning "algebra" (lit. "the science of calculation with elements" or the science of analytical calculation.") and avatamsa, meaning "a garland or any ring-shaped ornament", or "the crown." Bījaganitāvatamsa thus means "a garland of the elements of algebra" or "the crown of algebra."
The present name for the science of Bijaganita in English is algebra. Algebra is derived from al-jabr occurring occurring in the title of an Arabic book on Algebra by al Khwärizmi (died about 860 A.D.). As an operation, jabr denotes the transformation of a subtracted term to the other side of an equation and was used along with the three other operations, called mukhabalah, radd, and ikmal (or takmil), for solving algebraic equations.
The early (elementary) algebra was mostly the study of equations and methods for solving them while the modern (abstract) algebra is the study of mathematical structures, such as groups, rings, and fields.
Usually Hindu works on algebra, is divided into two parts, Part I dealing with algebraic-processes essential in solving algebraic equations (bijopayogi-ganita) and Part II dealing with algebraic equations (bija).
The Sanskrit text adopted here, is as found in the printed form, edited by Kripa Shankar Shukla which is based on an incomplete manuscript containing the whole of Part I and a few opening lines of part II, (and is incomplete).
Part I sets forth the following three topics:
(1) Algebraic operations (of addition, subtraction, multiplication, division, squaring and extracting the square-root) for each of the following:
(i) Positive and negative numbers (dhanarna),
(ii) The zero (sunya),
(iii) Single unknown (avyakta),
(iv) More unknowns characterized by colours(varna),
(v). surds (karaṇī).
(2) The Pulveriser (kuṭṭaka), i.e. analysis pertaining to the indeterminate equation (ax + c)/b=y.
(3) The Square-nature (varga-prakrti), i. e., analysis pertaining to the indeterminate equation :
Nx² + c = y².
The use of symbols - letters of the alphabet to denote unknowns - and equations are the foundations of the science of algebra. The Hindus were the first to make systematic use of the letters of the alphabet to denote unknowns. They were also the first to classify and make a detailed study of equations, Thus they may be said to have given birth to the modern science of algebra.
The Indian method of writing equations was better than the Chinese, and in one respect was the best that has ever been suggested. The method is a fine example of syncopated (or semi-symbolic) algebra and the style was uniformly used for more than a thousand years.
Indian algebra is especially noteworthy for its development of indeterminate analysis.
The famous Indian Cakravāla or Cyclic method for solving Nx² + 1 = y² was known to Jayadeva (c,1000) A.D.) or possibly to earlier Indians and is considered to be "certainly the finest thing which was achieved in the theory of numbers before Lagrange" (c. 1780).
A study of this book, Bijaganitāvatamsa, will reveal to the reader the remarkable progress in algebra made by the Hindus at an early date. It will also show that we are indebted to the Hindus for the technique and fundamental results of algebra just as we owe to them the place-value system in arithmetic, and invention of the basic function 'sine' in Trigonometry.
Engineer Venugopal D. Heroor is a very keen, enthusiastic and devoted scholar of Indian mathematics. He has already benefitted students, teachers and other scholars by his "The History of Mathematics & Mathematicians of India", "Bharatiya Trikonamiti Sastra", "Brahmagupta Ganitam", "Pātīganita Sāra", Bhāskriya Bījaganitam and several other books.
Readers (teachers, students, practitioners, historians etc.) will definitely find Er. Heroor's present book, Bījaganitāvatamsa also both charming and exciting as well as enlightening.
Nārāyaṇa Pandita (A.D. 1356):
Nārāyaṇa Daivajña or Nārāyaṇa Pandita as he was popularly called, was the son of Nrsimha Daivajña. He is solely a mathematician and the author of two works namely (i) Ganitakaumudi¹ (G.K.) a mathematical treatise in 14 chapters, and (ii) Bijaganitāvatamsa² a work on algebra. Besides these two works, Nārāyaṇa has also written a work on Sanskrit prosody viz. Manimanjarī ³ on Sanskrit prosody.
Comparison of the colphon giving the name of the author as Nārāyaṇa Pandita and that of his father as Nrsimha at the end of Part I of Bijaganitāvatamsa, with the colphons occuring at the end of the various sections of the Ganitakaumudi leaves little doubt that the author of the Bijaganitāvatamsa was the same Nārāyaṇa Pandita as the author of the Ganitakaumudī. The identity of the authors of the Ganitakaumudi and the Bijaganitāvatamsa is also established by the fact that most of the verses (including commentaries thereon) found in the sections dealing with kuṭṭaka and varga-prakrti in the two works are almost literally the same. There is also a reference in the Ganitakaumudi to the author's Bijaganita.
The verse occuring in the end of the Ganitakaumudi (G.K. Part II pp.410) shows that the author's father Narasimha (Skt. Nrsimha) was a respectable brahmaṇa well versed in Śrtis and Smrtis and a devotee of God Śiva and that besides being a good scholar of the Śästras, he had acquired a high degree of proficiency in the mechanical science, the science of arms (Sastras,) and logic.
Nārāyana Pandita lived in the fourteenth century of the Christian era. The concluding verse of the Ganitakaumudi shows that the Ganitakaumudi was completed on Thursday, the second tithi of the dark fortnight of the month Kārtika, Samvastara Durmukha, saka year 1278. This corresponds to Thursday, October 14, A.D.1356. The Bijaganitāvatamsa which is mentioned in the Ganitakaumudi was evidently written prior to this date.
It is not known where the author lived and worked, but the distribution of manuscripts indicates that he was possibly from North India.
Bijaganitāvatamsa:
The name Bijaganitävatamsa is a compound formed by the words Bijaganita, meaning "algebra" (lit. "the science of calculation with elements"), and avatamsa, meaning " a garland or any ring shaped ornament", or "the crown". Bijaganitāvatamsa thus means "a garland of the elements of algebra" or "The Crown Of Algebra".
The work availabale now, in printed form, published by Akhila Bharatiya Sanskrit Parishad, Lucknow, in 1970, is incomplete. It has been mentioned by the editor, Kripa Shankar Shukla, that the crtical edition brought out is based on an incomplete manuscript containing the whole of Part I and a few opening lines of part II, which was acquired by the late Dr. A. N. singh, belongs to their collection.
**Contents and Sample Pages**