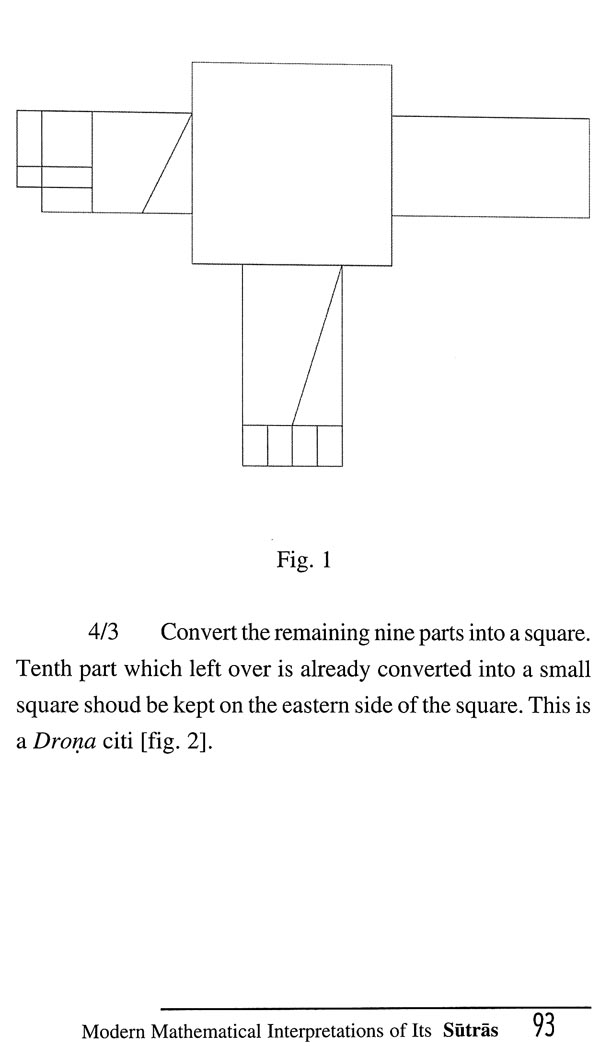
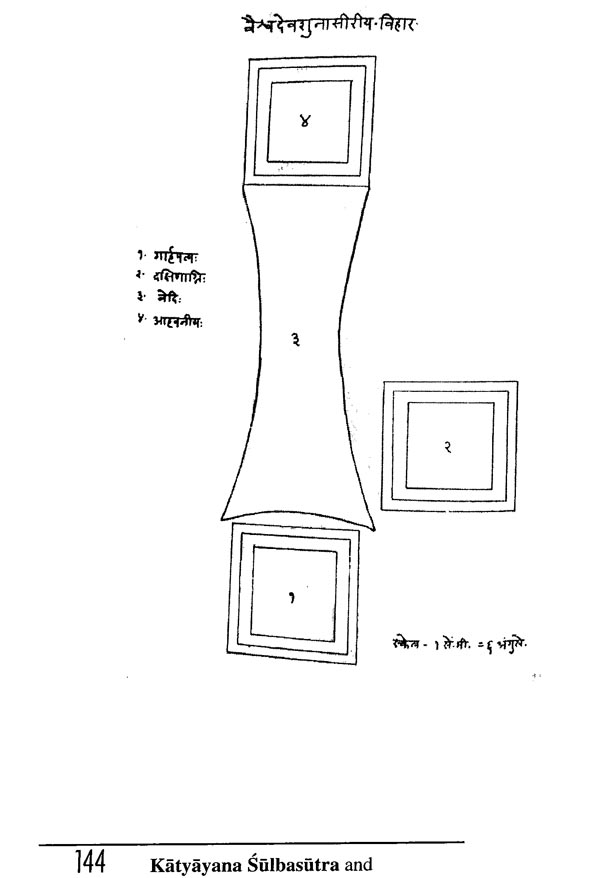
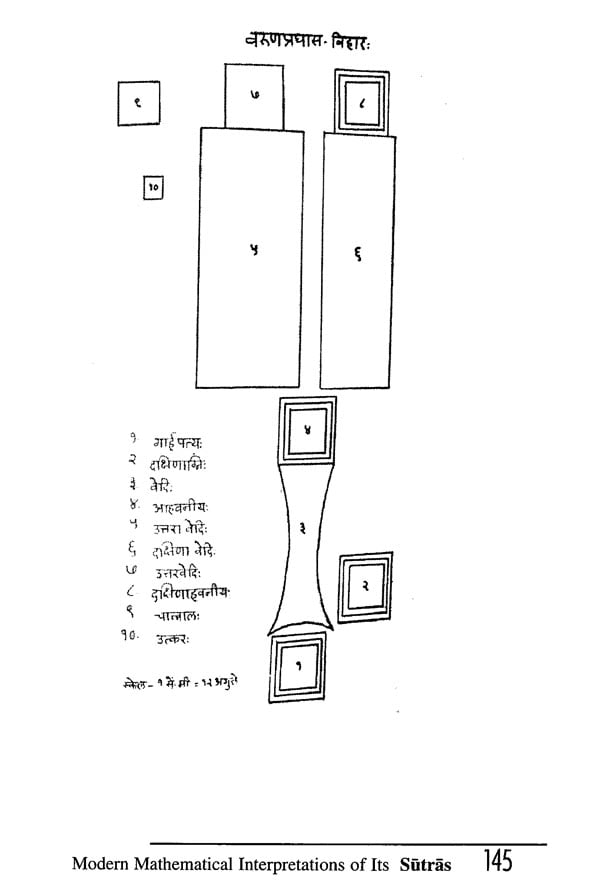
Katyayana Subasutra: and Modern Mathematical Interpretations of its Sutras

Preface In retrospect, I remember the year 1995, the year of my first encounter with Vedic mathematical approaches and devices when I came to Gurukul Kangri Vishwavidyalaya, Haridwar. I had an opportunity to interact with many of the scholars of mathematics, who were involved in studies of mathematics in vedic traditions. The perusal of the studies on the subject raised several questions in my mind as to the distinct identity of mathematics in vedic traditions and its scope in modern times. This inquisitiveness impelled me to write my doctoral dissertation on some aspects of mathematics in vedic traditions.

I am greatly obliged to Lt. Prof. Ramesh Chandra Dash Sharma, Deptt. of Veda, Shri Lal Bahadur Shastri Rashtriya Sanskrit Vidyapeetha, (Deemed University) New Delhi, who inspired me to make the Sulbsutra the integral part of my research. There are many commentators of Katyayana Sulbsutra e.g. Gangadhar, Karkmahidhar, Ramchandra & Prof. R.C.D. Sharma. For my study I selected the commentary by Lt. Prof. R.C.D. Sharma.

Sulba which literary means 'Science of Measurement'. This research mainly reveals the mathematical construction of Vedic, Mandaparn, and alters for fulfilment of various desire. My research reveals the ancient ways of measurement which are measured from the different part of body. i.e. arathni angula etc. During those ancient days it was not possible to construct the altars without the help of mathematicians. Only an altar made with accurate area could help in fulfilling the desired wish. Place of Eulbsrara has been very important for vedic ceremonies. „culbs'atra are intended to lay down the rules of demarcation of various sacrificial altars, Kimda and mandapa, places for sacred fire etc. provided according to directions quoted in Vedas and grautasittra for performing various rituals.

Some of the background research for this work was carried out during the course of research at Vaidik SanSvdhana Mandala, Hoshiarpur (1997) and at Delhi.

Looking vedic mathematics with new insight (as in respect to cosmic world) I tried to touch hidden part of nature. In my study I found that there is correlation between human body and Yapia being performed by us and the universe. Of course the desired result can be obtained only if it is done in a very accurate calculative & mathematical way. I tried to reveal unsolved theories, which require more research to benefit the mankind.

My greatest debts are towards my guide Late Prof. V.K. Arora and my teacher Late Prof S.L. Singh. His monumental erudition and wisdom nourished the study of history of Indian exact sciences for nearly half a century and his passing away is an irreparable loss to field.

My sincere thanks to Mr. Rakesh Manocha of Manyata Prakashan, Delhi who bore a large share of burden in the matter of printing and publishing my work.

Introduction Abstract

Introduction procedure for performing sacrifices and ceremonies are spread over Grhyasfitras literature. Kalpa literature is divided into two portions, viz, Grhyasutras and, i-autasutras. the rules relating to construction and transformation of various figures pertaining to shapes of altars and other mathematical detais as found in graittasutras were later on elaborated in much extent. This systematized and extended version assumed the form known as §ulbasutras (i.e. rules of chord which is now a part of Geometry). This chapter highlights the measuring contents of S'ulbasiitras and extends its advancement in world geometry.

Book's Contents and Sample Pages