Geometry in Ancient and Medieval India
Book Specification
| Item Code: | NAC168 |
| Author: | Dr. T.A. Sarasvati Amma |
| Publisher: | MOTILAL BANARSIDASS PUBLISHERS PVT. LTD. |
| Edition: | 2017 |
| ISBN: | 9788120813441 |
| Pages: | 278 |
| Cover: | Hardcover |
| Other Details | 8.8 inch X 5.8 inch |
| Weight | 500 gm |
Book Description
Book is a geometrical survey of the Samskrt and Prakrt scientific and quasi-scientific literature of India beginning with the Vedic literature and ending with the early part of the 17th century. It deals in detail with the Sulbasutras in the Vedic literature, with the mathematical parts of Jaina works and of the Hindu and with the contributions to geometry made by the astronomer- mathematicians Aryabhata I & II, Sripati, Bhaskara I & II, Sangamagrama Madhava, Paramesvara, Nilakantha, his disciples and a host of others. The works of the mathematicians Mahavira, Sridhara and Narayana Pandita and the Bakshali Manuscript have also been studied.
The work seeks to explode the theory that the Indian mathematical genius was predominantly algebraic and computational and that it eschewed proofs and rationales. There was a school in India which delighted to demonstrate even algebraical results geometrically. In their search for a sufficiently good approximation for the value of p Indian mathematicians had discovered the tool of integration, which they used equally effectively for finding the surface area and volume of a sphere and in other fields. This discovery of integration was the sequel of the inextricable blending of geometry and series mathematics.
About the Author
Dr. T.A. Saraswati Amma took her basic degree in Physics and Mathematics from the University of Madras. She took her Master’s degree in Sanskrit from B.H.U. and her Master’s degree in English Literature from Bihar University.
This book is her doctoral thesis on which she was awarded the Ph.D. degree by Ranchi University. Equipped as she is with a good knowledge of, both Mathematics and Sanskrit she was eminently suitable to carry on research on this very important topic.
She has made extensive contributions in the field of Sanskrit and Mathematics by way of publications, papers, post-doctoral research and participation in various national and international conferences.
Foreword
When the author of the present Thesis came y to me to do research, I did not want her to take up any subject in the over- worked fields of Alamkara, Vedanta or general literature and wanted to know if she was prepared, to work in fields which were neglected or in which few young scholars were inclined to put forth their efforts. On further enquiry I found that she was qualified in mathematics, having taken her first degree in physics and mathematics and decided that she should specialise in the field of Indian contribution to mathematics, algebra and geometry.
The originality and antiquity of Indian contribution to these branches of science have been questioned by some of the historians of mathematics. For example while it is generally believed that the credit of having discovered the place value and decimal system goes to India, some distinguished modern writers do not accept this. But in the case of geometry, we are on more Solid grounds. Not only are the Sulba Sutra earlier in date to Pythagoras but the entire sacrificial system and the fire altars, vedic for which the Sulba Sutras were intended, are already pre- supposed by the Rigvedic hymns. The biased view of the ancient Hindu contribution, either for or against, has been aggravated, as observed by an eminent modern Indian scientist, by the inadequate publication of the original documents. Needham says "future research on the history of science and technology in Asia, will, in fact, reveal that the achievements of these peoples contribute far more, in all pre-renaissance periods, to the development of world science than has yet been realised." This study to be useful could be undertaken only by those who have scientific equipment, and if these have the additional grounding of a knowledge of Sanskrit, the best possible results could be! expected. The material available should be interpreted in terms of modern knowledge in the concerned sciences. It is in this respect that work such as the one being introduced here is important.
Dr. Sarasvati has examined ancient Indian geometry as seen in the Vedic period and its Sulba Sutras and in the texts of the classical and post-classical periods of Sanskrit literature, as also in the Jain texts like the Surya, Candra and Jambudvipa Prajnaptis. The work was recommended for the Doctorate Degree by Judges who were mathematicians and its publication will be an addition to the meagre expositions available on the scientific aspects of Sanskrit literature.
The efforts of the section of the Ministry of Education dealing with the history of Science in India and of the Association for the History of Science and their Journal have been helpful for the development of researches in this field. Special emphasis was laid by the First International Sanskrit Conference held recently by the Ministry of Education, on Sanskrit and Science and Technology and it revealed the talent available for tackling subjects in this area. However it cannot be said that, as in the case of Philosophy, Professors of the different sciences in the Indian Universities have become interested in this subject; as I have pleaded the history in India of the respective sciences should form a regular complementary part of the study of modern sciences in the Universities and should form legitimate subjects for research degrees for Science graduates.
I hope that the author will continue her investigations in this specialised field and will make further contributions to the elucidation of the Sanskrit literature on mathematics.
Preface
This book is the third in a series of books on Indian Mathematics. The first two, History of Hindu Mathematics by B.B. Datta and A.N. Singh, Part I first published in 1935 and Part II published in 1938, concern themselves with Arithmetic and Algebra in Pre-British India. The present book, the author’s doctoral thesis, has geometry in the India of the same period as its theme. A similar history of Indian Trigonometry has been compiled by Dr. R.C. Gupta of the Birla Institute of Technology as his doctoral thesis under the guidance of the present author, who has also collected some materials for a history of series Mathematics in India. She hopes to be able to present them in a book form before the research world. A comprehensive history of Indian astronomy is another desideratum to complete the picture of the development of Mathematics in ancient and medieval India.
Indeed the last one should have been the nucleus around which the other sections are to be grouped. For, at least after the Sulbasutra period, the main developments in Indian mathematics were oriented towards and inspired by the needs of astronomy. The word, Jyotisa (the science of the luminaries) covered all branches of mathematics The word, ‘ganita’ (calculations) which combined with Pati (calculating board), Bija (algebraical elements) and Ksetra (held or figure), denotes arithmetic, algebra and geometry respectively has also got an astronomical colouring, since the root ‘gan’ has always had a Special association with astronomical computations.
Geometry, as remarked above, is designated as Ksetragainita in most Indian mathematical works. Ksetra means a closed figure whether it be a field or a figure drawn on the calculating board. In the Sulbasutras and in the Buddhist works rajju or Pujjuganita (calculations with the cord) stands for geometrical Calculations. It is only very late that we come across the use of the term Rekhaganita, calculations connected with the line.
Ksetraganita does not include the calculation of volumes, which is generally given under a separate heading Khatavyavahara section dealing with excavations. Rasiganita, calculations connected with heaps also has some geometrical interest. The present work is mainly based on the Ksetra and Khata sections of available mathematical texts, Rasiganita is rarely made use of, since these calculations are usually approximations. Most astronomical calculations being based on geometry, the purely astronomical texts also will yield geometrical material. But such material is not included in this study. In some of the texts like the Ganitasarasamgraha, Mahasiddhanta and the Ganitakaumudi rules or formulae are given for computing the areas of figures which are not basic geometric, figures, but which can be cut up into basic geometric figures like the segment and the triangle. Examples are the figures called Yam (barley corn), muraja (a sort of drum) and Sabkha (conch shell). These are also omitted in this study unless they have some special geometrical interest.
The completion of this work as planned is primarily due to the help and encouragement received from my guide, Dr. V. Raghavan, Professor of Sanskrit (since retired), Madras University. I am extremely grateful for his guidance and for gracing this book with his valuable Foreword. I also acknowledge with grateful thanks the help given to me by Prof. T.S. Kuppanna Sastrigal, retired Professor of Sanskrit, Sanskrit College, Madras, Dr. K. Kunchunni Raja, Professor of Sanskrit, Madras University, Prof. C.T. Rajagopal, retired Director, Ramanujam Institute, Madras, Sri Rama Verma (Maru) Tampuran (Joint editor of the Yuktibhasa), Dr. K.V. Sharma, (now) Reader in Sanskrit, Punjab University, in procuring books and manuscripts- and in unravelling the meaning of obscure mathematical passages, and the help of my friends and colleagues Smt. C. P. Parvati, Smt. Helen Barnard and Sri K. R. Prabhakar in correcting the typescript and in typing and proof—reading.
I thank the Government of India for granting me a Humanities Research Scholarship and for sanctioning 50% of the publication cost, though I could not make use of the promised help in time and so forfeited it. I am grateful to the Ranchi University for subsidising this publication in part and to Motilal Banarsidass, Publishers and Book-sellers, for bringing out this work, which, by its very nature, has scant commercial value.
Excerpts from reviews:
“The book under review is an almost exhaustive survey of geometry in Sanskrit and Prakrit literature right from the vedic times down to the early part of the seventeenth century A.D. The contributions to geometry made by Sulba Sutras, Hindu The contributions to geometry made by Sulba Sutras, Hindu Siddhanta, Jaina Canonical works, Bakshali manuscript as also by eminent mathematicians, Aryabhata I & II, Sripati, Bhaskaracharya I & II, Mahavira, Sridhara, Nilakanta and a few others have been dealt with critically.
The present book has filled more than adequately the long gap after the publication of an equally authentic, exhaustive source book, History of Hindu Mathematics in two Volumes (1935-1938), by B.B. Datta and A.N. Singh, which deals with ancient Indian arithmetic and algebra.”
Deccan Herald Magazine,
Sunday, October 21, 1979
“An admirable feature of the book is the impartial scholarly attitude to the study and a complete absence of parochialism. The book is supplemented with an exhaustive Bibliography, a Glossary of Geometrical Terms and an Index.
A higly commendable treatise, the work is very useful as a text book of Hindu geometry.”
Annals of B.O.R. Institure
Vol. LXIX (1988), Poona 1988.
“This book is a geometrical survey of Sanskrit and Prakrit scientific literature beginning from the Sulba-sutras (VIth-Vth century B.C.) and ending with the early of XVIIth century A.D…
As pointed out by the author in the preface “the book is the third in a series of books on Indian mathematics….In fact, this book considerably.”
CONTENTS
| Foreword V. Raghvan | v |
| Preface | vii |
| Chapter I. Introduction | 1 |
| Geometry as the branch of Indian mathematics with the earliest recorded development - the change from constructional character to circle-orientedness - lack of proofs explained - utilitarian character of Indian mathematics - general survey of the history of geometry and mathematics in India. | |
| Chapter II. Sulbasutra Geometry | 14 |
| The number of Sulbasutras - their date - the term sulba - analysis of the contents of the Sulbasutras - the theorem of the square of the diagonal - determining the east-west line - to draw the perpendicular bisector of a given line - construction of squares, rectangles and trapezia - transformation of figures - combination and subtraction of areas - geometrical truths implied in the constructions - properties of similar figures - areas - rational right triangles - early geometrical terminology - the Sulbasutras and later ages. | |
| Chapter III. Early Jaina Geometry | 61 |
| The impetus for the study of geometry - the very early works - the value 10 for solid figures - the trapezium and the trapezoidal solid. | |
| Chapter IV. The Trapezium | 70 |
| The treatment in early Jaina literature, by Aryabhata I, by Brahmagupta, by Sridhara, by Mahavira, by later Jaina authors, by Aryabhata II, by Sripati, by Bhaskara II, by Narayana Pandit. | |
| Chapter V. The Quadrilateral | 81 |
| The cyclic quadrilateral verses the non-cyclic-Suciksetras - non-cyclic quadrilaterals - Narayana Pandit’s treatment of the cyclic quadrilateral - Paramesvara’s expression for the circumradius and the Kriyakramakari proof for it - the Yuktibhasa proof for trigonometrical identities and for Brahmagupta’s expressions for the diagonals and area of a cyclic quadrilateral. | |
| Chapter VI. The Triangle | 117 |
| Early mention of - treatment by Aryabhata, by Brahmagupta etc. - Nilakantha’s logical demonstration for the concurrence of the perpendicular bisectors of a triangle - the theorem of the square on the hypotenuse and its proof.-rational rectilinear figures - the rational cyclic quadrilateral - Narayana’s treatment of the rational trapezium-the rational right triangle in the Aryabhata school. | |
| Chapter VII. The Circle | 154 |
| The circle in early work - Aryabhata I’s value of p by the method of exhaustion - series for p and close approximations to the value of p - finding the area of a circle - the segment and the chord - Madhava’s discovery of Gregory’s series - the common chord and its arrows - inscribed polygons - mutually touching circles. | |
| Chapter VIII. Volumes and Surfaces of Solids | 195 |
| Volume in early works - the pyramid - Aryabhata I’s rue for the volume of a tetrahedron - pyramid-frustum and con-frustum - the sphere - the surface-area and volume of a sphere by integration. | |
| Chapter IX. Geometrical Algebra | 218 |
| In the Sulbasutras - in the commentaries of Bhaskara II’s works - in the Aryabhata School Citrabhanu’s geometrical demonstrations of algebraical identities - sredhiksetras. | |
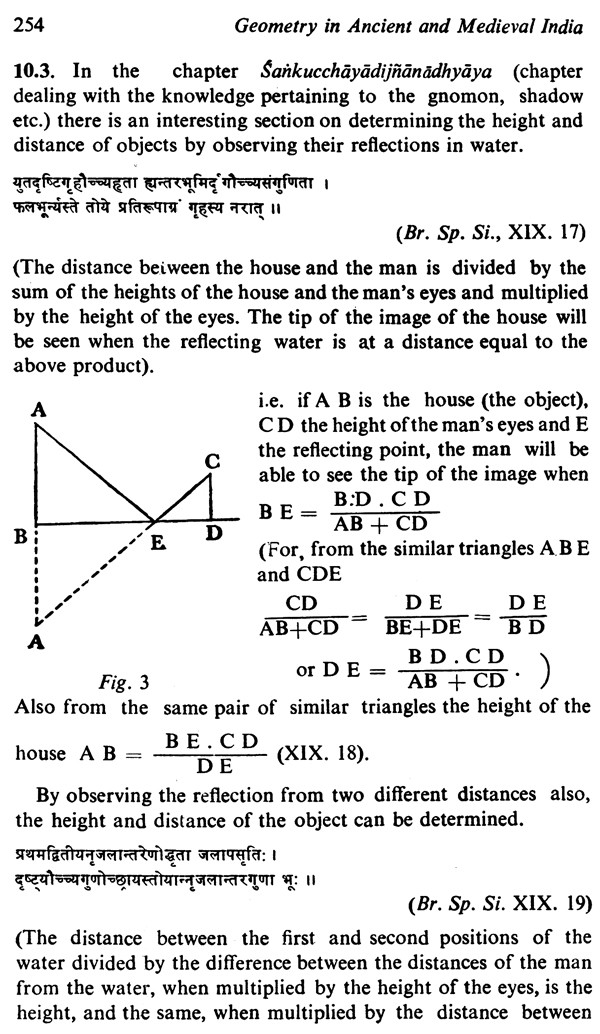
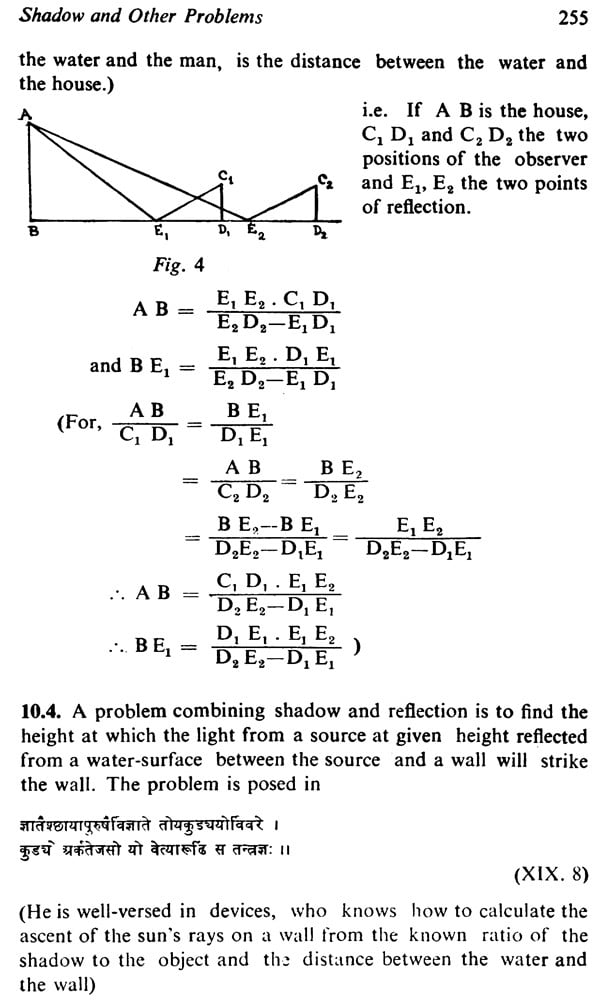
| Chapter X. Shadow problems and other problems | 251 |
| Glossary of Geometrical Terms | 261 |
| Bibliography | 267 |
| Index | 273 |